What is a exponential function ?
Think of it like a convience tool for repeated multiplication, we have a base and a exponent the exponent tell us how many times we are to multiply the base with itself
\[\\ y = b^x = \underbrace{b \cdot b \cdot \dots \cdot b}_{x \text{ times}}\]Rules
Rules for the Exponent (\(x\))
- Positive Exponent (\(x > 0\)): Repeated multiplication.
- Example: \(2^3 = 2 \cdot 2 \cdot 2 = 8\)
- Zero Exponent (\(x=0\)): The result is just 1. It’s the identity or starting point before any multiplication. \(b^0 = 1\)
- Negative Exponent (\(x < 0\)): It means “reciprocal” or “flip.” \(b^{-x} = \frac{1}{b^x}\)
- Example: \(2^{-3} = \frac{1}{2^3} = \frac{1}{8} = 0.125\)
Rules for the Base (\(b\))
- The base \(b > 0\) (must be positive). We do this to ensure the function gives real number outputs for all real exponents \(x\) and avoid complex numbers (like \(\sqrt{-1}\)) that arise from roots of negative numbers.
- The base \(b \neq 1\). If \(b=1\), then \(y = 1^x = 1\), which is just a constant flat line, not an exponential function.
- If \(b > 1\), we get exponential growth.
- If \(0 < b < 1\), we get exponential decay.
The Graph
Positive Exponents (Growth)
This plot shows \(y = 2^x\) for \(x \ge 0\). Notice it passes through \((0, 1)\) and grows rapidly.
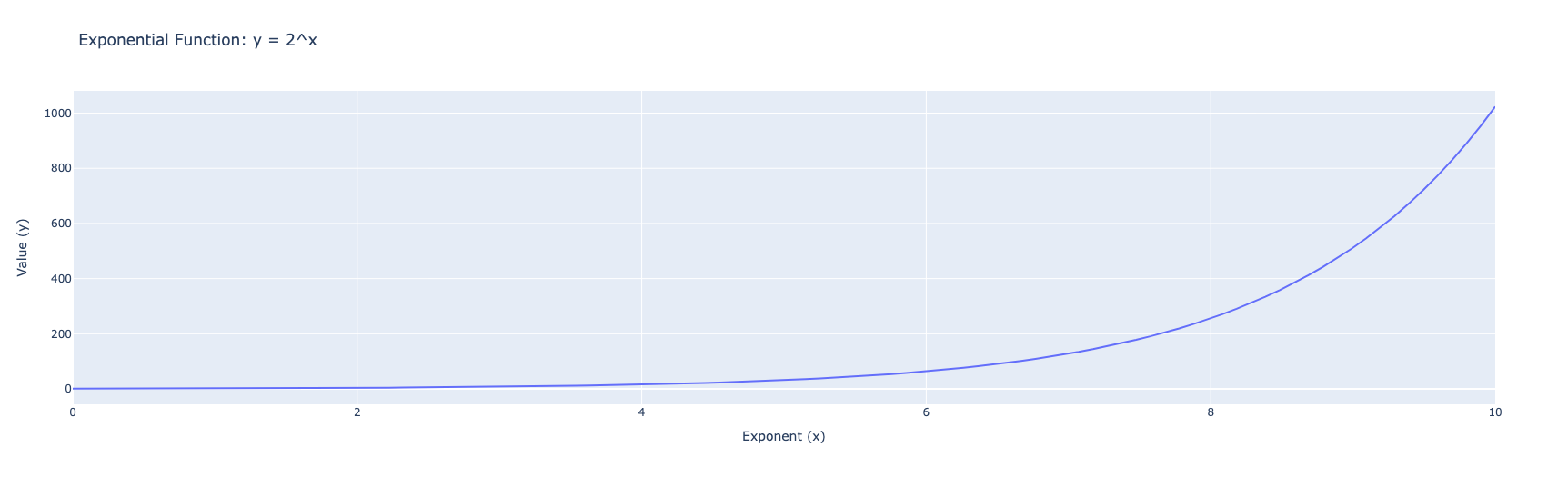
Negative Exponents (Approaching Zero)
When we make the exponent negative, the function approaches zero but never reaches it.
Example for \(x = -9999\) and \(b = 2\):
\[y = 2^{-9999} = \frac{1}{2^{9999}} \approx 0 \text{ (but never exactly 0)}\]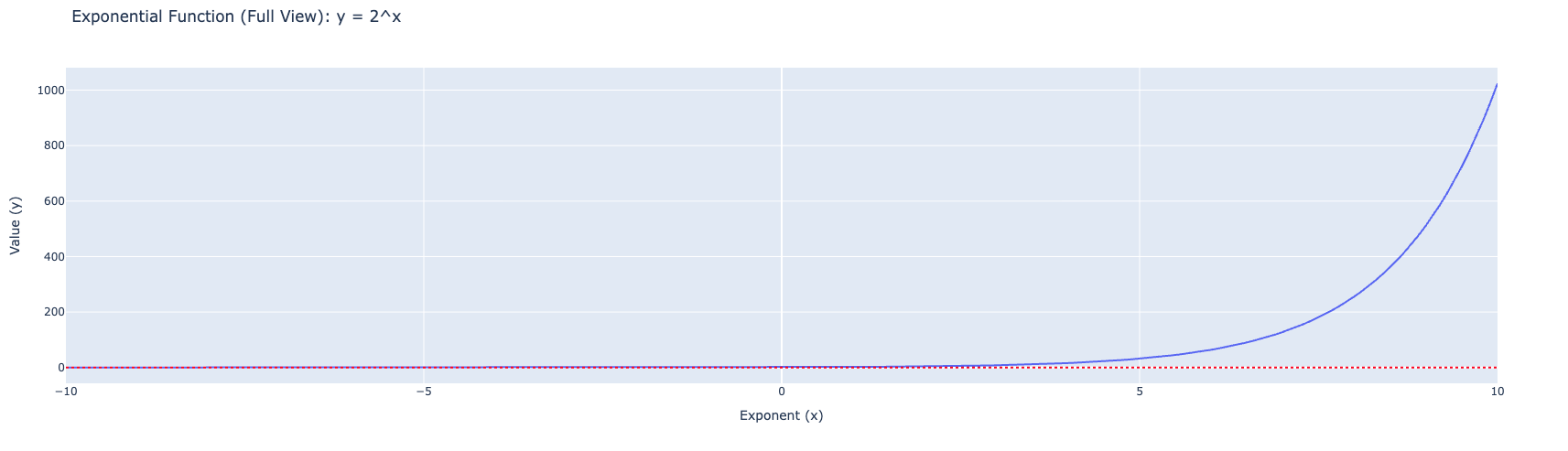
This is why the graph gets infinitely close to the x-axis on the left side (as \(x \to -\infty\)). This is a horizontal asymptote.