Table of Contents
Task Scenario
A Simple 2-Revolute Robotic Arm Manuever: Reaching for the Shelf.
Imagine a 2-joint robotic arm resting flat on a table. An object sits to its left on a nearby shelf. The arm needs to rotate and bend to probe or grab it.
Animation:
Mathematical Model
The fun part
Let’s start with a unit representation. Suppose we have a vector:
\[\vec{a} = (x, y, z)\]and we want to rotate it by an arbitrary angle \(\theta\).
1. Rotation about the origin
When the pivot point is at the origin, the rotation is straightforward. We apply the rotation matrix directly to the vector:
\[\vec{a}' = R(\theta) \cdot \vec{a}\]where \(R(\theta)\) is the rotation matrix corresponding to the desired angle \(\theta\).
2. Rotation about a point other than the origin
When the pivot point is not at the origin, the process involves three steps:
- Translate the vector so that the pivot point moves to the origin.
- Rotate the vector around the origin.
- Translate the vector back to its original position.
This can be expressed as:
\[\vec{a}' = T(p) \cdot R(\theta) \cdot T(-p) \cdot \vec{a}\]where:
- \(T(p)\) is the translation matrix that moves the pivot point \(p\) to the origin.
- \(R(\theta)\) is the rotation matrix for the angle \(\theta\).
- \(T(-p)\) is the translation matrix that moves the vector back after rotation.
This process ensures that the vector rotates around the desired pivot point.
Rotation matrices
Using the right-hand rule (positive \(\theta\) means counterclockwise rotation when looking along the positive axis):
\[R_z(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}\] \[R_y(\theta) = \begin{bmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{bmatrix}\] \[R_x(\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix}\]Translation vector
A translation in 3D is represented as:
\[\mathbf{T} = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}\]Combining rotation and translation
We use homogeneous coordinates to apply rotation and translation in one step.
With column vectors and the convention \(\mathbf{p}' = \mathbf{M}\,\mathbf{p}\):
A rigid-body transformation that first rotates, then translates, is:
\[\mathbf{M} = \begin{bmatrix} R & \mathbf{T} \\ \mathbf{0}_{1\times3} & 1 \end{bmatrix}\]For example, rotation about the \(z\)-axis by \(\theta\):
\[\mathbf{M} = \begin{bmatrix} \cos\theta & -\sin\theta & 0 & t_x \\ \sin\theta & \cos\theta & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}\]The transformation
Multiplying:
\[\mathbf{p}' = \mathbf{M}\,\mathbf{p}\]gives:
\(\mathbf{p}' = \begin{bmatrix} R\,\mathbf{p}_{xyz} + \mathbf{T} \\ 1 \end{bmatrix}\) where \(\mathbf{p}_{xyz} = \begin{bmatrix} x \\ y \\ z \end{bmatrix}\)
Note on order:
Rotation then translation is not the same as translation then rotation.
Let’s plug in our configuration
Physical Setup (Initial State)
- World Origin: Coordinates: \((0, 0, 0)\)
- Base: Coordinates: \((0, 0, 0)\)
- Joint 1 Origin (J1) Base Joint
- Located at the World Origin \((0, 0, 0)\)
- Rotates about the table’s Z-axis
- Link 1 Origin (L1) First Arm Segment
- Origin is at J1’s position \((0, 0, 0)\)
- Extends 5 units along the +X axis in the world frame
- Joint 2 Origin (J2) Elbow Joint
- Located at the end of Link 1
- Coordinates: \((5, 0, 0)\) in the World frame initially
- Rotates about its local Z-axis (relative to Link 1’s orientation)
- Link 2 Origin (L2) Second Arm Segment
- Origin is at J2’s position
- Extends 4 units along its own local +X direction.
- End-Effector (EE) Gripper/Probe
- Located at the end of Link 2
- Initial coordinates: \((9, 0, 0)\) in the World frame
Give we are using a 4x4 matrix, we augment out vector descriptions with an additional dimension to work with the transformation matrix.
Code
The initial description:
world_origin = np.array([0, 0, 0, 1])
joint_one_origin = world_origin.copy()
link_one_origin = joint_one_origin + np.array([5, 0, 0, 0])
joint_two_origin = joint_one_origin + np.array([5, 0, 0, 0])
link_two_origin = joint_two_origin + np.array([4, 0, 0, 0])
# robot configuration
robot_configuration = {
'world_origin': world_origin,
'joint_one_origin': joint_one_origin,
'link_one_origin': link_one_origin,
'joint_two_origin': joint_two_origin,
'link_two_origin': link_two_origin
}
Utility functions:
import numpy as np
from math import cos, sin, radians
from typing import Tuple
from enum import Enum
class AxesOfRotation(Enum):
X = 'X'
Y = 'Y'
Z = 'Z'
def getTranslationMatrix(translation: Tuple[float, float, float]) -> np.ndarray:
tx, ty, tz = translation
return np.array([
[1, 0, 0, tx],
[0, 1, 0, ty],
[0, 0, 1, tz],
[0, 0, 0, 1]
])
def getRotationMatrix(axesOfRotation: AxesOfRotation, theta: float) -> np.ndarray:
c, s = cos(theta), sin(theta)
if axesOfRotation == AxesOfRotation.X:
return np.array([
[1, 0, 0, 0],
[0, c, -s, 0],
[0, s, c, 0],
[0, 0, 0, 1]
])
elif axesOfRotation == AxesOfRotation.Y:
return np.array([
[ c, 0, s, 0],
[ 0, 1, 0, 0],
[-s, 0, c, 0],
[ 0, 0, 0, 1]
])
elif axesOfRotation == AxesOfRotation.Z:
return np.array([
[c, -s, 0, 0],
[s, c, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
])
else:
raise ValueError("Where we at?")
def getTransformationMatrix(axesOfRotation: AxesOfRotation, theta: float,
pivot: Tuple[float, float, float] = (0,0,0),
translation: Tuple[float, float, float] = (0,0,0)
) -> np.ndarray:
T_neg_pivot = getTranslationMatrix((-pivot[0], -pivot[1], -pivot[2]))
R = getRotationMatrix(axesOfRotation, theta)
T_pivot = getTranslationMatrix(pivot)
M = T_pivot @ R @ T_neg_pivot
return M
Performing our manuevers
Manuever 1:
# Manuever 1: Rotate joint 1 by 90 degrees about Z axis, pivot at joint_one_origin (the hinge)
rotation_1_rad = radians(90)
pivot_1 = joint_one_origin[:3]
rotation_matrix_1 = getTransformationMatrix(
AxesOfRotation.Z,
rotation_1_rad,
pivot=pivot_1
)
joint_one_origin_rotated_1 = rotation_matrix_1 @ joint_one_origin
link_one_origin_rotated_1 = rotation_matrix_1 @ link_one_origin
joint_two_origin_rotated_1 = rotation_matrix_1 @ joint_two_origin
link_two_origin_rotated_1 = rotation_matrix_1 @ link_two_origin
rotated_origin_vectors = {
'joint_one_origin_rotated_1': joint_one_origin_rotated_1,
'link_one_origin_rotated_1': link_one_origin_rotated_1,
'joint_two_origin_rotated_1': joint_two_origin_rotated_1,
'link_two_origin_rotated_1': link_two_origin_rotated_1
}
#After manuever 1, the positions are
#Note: Floating Point Precision values like e-16 are approximately zero
joint_one_origin_rotated_1: [0. 0. 0. 1.]
link_one_origin_rotated_1: [3.061617e-16 5.000000e+00 0.000000e+00 1.000000e+00]
joint_two_origin_rotated_1: [3.061617e-16 5.000000e+00 0.000000e+00 1.000000e+00]
link_two_origin_rotated_1: [5.5109106e-16 9.0000000e+00 0.0000000e+00 1.0000000e+00]
Manuever 2:
# Manuever 2: Rotate joint 2 by 45 deg about the z axis
rotation_2_rad = radians(45)
pivot_2 = joint_two_origin_rotated_1[:3]
rotation_matrix_2 = getTransformationMatrix(
AxesOfRotation.Z,
rotation_2_rad,
pivot=pivot_2
)
joint_two_origin_rotated_2 = rotation_matrix_2 @ joint_two_origin_rotated_1
link_two_origin_rotated_2 = rotation_matrix_2 @ link_two_origin_rotated_1
#After manuever 2, the positions are
#Note: Floating Point Precision values like e-16 are approximately zero
joint_one_origin_rotated_1: [0. 0. 0. 1.]
link_one_origin_rotated_1: [3.061617e-16 5.000000e+00 0.000000e+00 1.000000e+00]
joint_two_origin_rotated_2: [6.60578224e-16 5.00000000e+00 0.00000000e+00 1.00000000e+00]
link_two_origin_rotated_2: [-2.82842712 7.82842712 0. 1. ]
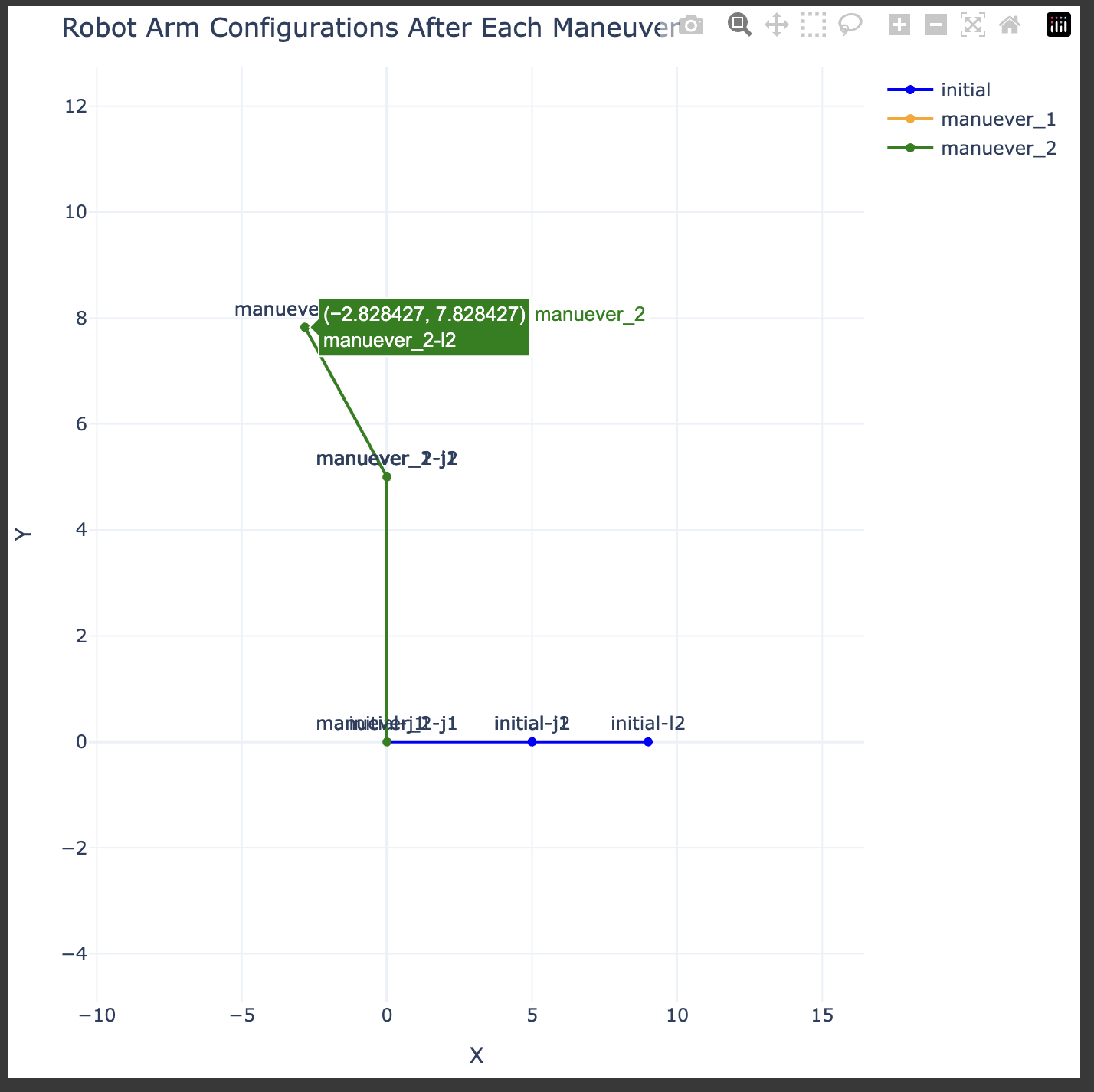
Plot: